Alpha Zero has recently changed the state-of-the-art of Artificial Intelligence (AI) performance in the game of Go, Chess and Shogi. In this blog post, I have implemented the AlphaZero algorithm for single player games. There are a few small modifications on my side to make it suitable for this setting, but these are rather small and explicitly mentioned in the text below. The core functionality (except some generic helper functions) takes merely ~250 lines of annoted Python code (including blank lines), contained in a single script. The main point of this blog post is to illustrate the potential simplicity of an AlphaZero implementation, and provide a baseline for interested people to experiment with.

Full code is available from www.github.com/tmoer/alphazero_singleplayer.git

Alpha Zero

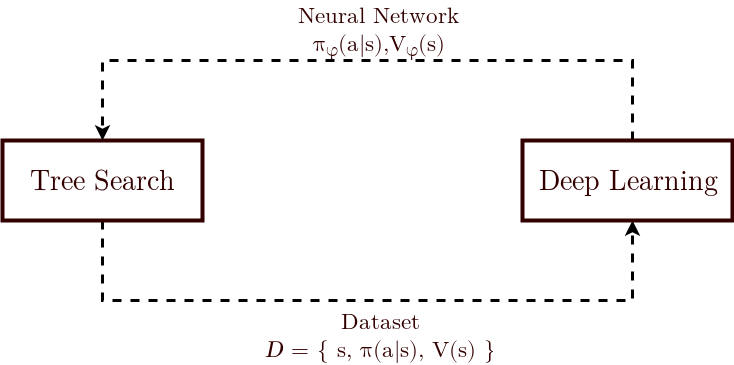
Probably the key-innovation of Alpha Zero is the iterated application of Monte Carlo Tree Search and Deep Learning. In most of standard reinforcement learning, which is grounded in instrumental conditioning, we usually take a single step or a single forward trace in the domain, which is then used to improve our policy (usually by training a neural network). The key idea of Alpha Zero is to store information locally a bit longer, by building a (small) local search tree, and only then train a network. At the end of this blog post I formulate a few hypothesis of why this works so well.

Python Implementation

We introduce the implementation around three core objects:

1. Model, which defines the neural networks (policy and value network)
2. MCTS, which specifies the Monte Carlo Tree Search procedure
3. Agent, which wraps the overall training process, iterating MCTS and neural network training.

Along the way, we also discuss the connections between MCTS and neural network training:

1. How we compute training targets from the MCTS procedure.
2. How the neural networks influence next tree searches (through a policy prior in the UCT formula, and by replacing a rollout by a bootstrap value network prediction).

Neural Networks

We start by defining our policy and value networks. We will wrap the definition in a Model object. This implementation assumes a 1D state space. If your input has more structure (e.g. in visual tasks), you may want to modify the feedforward/representation layers by adding convolutions (slim.conv2d()) etc.

class Model():
    
    def __init__(self,Env,lr,n_hidden_layers,n_hidden_units):
        # Check the Gym environment
        self.action_dim, self.action_discrete  = check_space(Env.action_space)
        self.state_dim, self.state_discrete  = check_space(Env.observation_space)
        if not self.action_discrete: 
            raise ValueError('Continuous action space not implemented')
        
        # Placeholders
        if not self.state_discrete:
            self.x = x = tf.placeholder("float32", shape=np.append(None,self.state_dim),name='x') # state  
        else:
            self.x = x = tf.placeholder("int32", shape=np.append(None,1)) # state
            x =  tf.squeeze(tf.one_hot(x,self.state_dim,axis=1),axis=2)
        
        # Feedforward: Can be modified to any representation function, e.g. convolutions, residual networks, etc. 
        for i in range(n_hidden_layers):
            x = slim.fully_connected(x,n_hidden_units,activation_fn=tf.nn.elu)
            
        # Output
        log_pi_hat = slim.fully_connected(x,self.action_dim,activation_fn=None) 
        self.pi_hat = tf.nn.softmax(log_pi_hat) # policy head           
        self.V_hat = slim.fully_connected(x,1,activation_fn=None) # value head

        # Loss
        self.V = tf.placeholder("float32", shape=[None,1],name='V')
        self.pi = tf.placeholder("float32", shape=[None,self.action_dim],name='pi')
        self.V_loss = tf.losses.mean_squared_error(labels=self.V,predictions=self.V_hat)
        self.pi_loss = tf.nn.softmax_cross_entropy_with_logits_v2(labels=self.pi,logits=log_pi_hat)
        self.loss = self.V_loss + tf.reduce_mean(self.pi_loss)
        
        self.lr = tf.Variable(lr,name="learning_rate",trainable=False)
        optimizer = tf.train.RMSPropOptimizer(learning_rate=lr)
        self.train_op = optimizer.minimize(self.loss)
    
    def train(self,sb,Vb,pib):
        self.sess.run(self.train_op,feed_dict={self.x:sb,
                                          self.V:Vb,
                                          self.pi:pib})
    
    def predict_V(self,s):
        return self.sess.run(self.V_hat,feed_dict={self.x:s})
        
    def predict_pi(self,s):
        return self.sess.run(self.pi_hat,feed_dict={self.x:s})

Monte Carlo Tree Search

First we define our State and Action objects (code directly below), from which we will built our MCTS tree. Both of these objects are fairly standard. The only difference compared to standard MCTS is:

1. The select step (UCT formula) in State.select(): For each child action, we now evaluate child_action.Q + prior * c * (np.sqrt(self.n + 1)/(child_action.n + 1)). Compared to the standard UCT equation, the denominator of the second term contains a +1, and the second term is scaled by the prior as obtained from the policy network. I added the + 1 term in the numerator myself, to prevent the first select action from being randomly selected (else the complete second term collapses to 0 for all actions).
2. The initialization of the mean action value in Action.__init__(): In this implementation we initialize each Q(s,a) to the value of state s, as bootstrapped from the neural network (self.Q = Q_init). Note that this is a modification of the original AlphaZero algorithm, which always initializes the tree search means at Q(s,a) = 0. However, as opposed to two-player board games which are either won or lost (total return 0 or 1), in many single player games the scale of the returns can vary much more. Therefore, the initial guess of 0 may be much too low or high, thereby creating too little or much exploration on the first visits, respectively. The value network provides a better estimate of the mean value of each action, so we instead use this prediction as the initial guess.

class State():
    ''' State object '''

    def __init__(self,index,r,terminal,parent_action,na,model):
        ''' Initialize a new state '''
        self.index = index # state
        self.r = r # reward upon arriving in this state
        self.terminal = terminal # whether the domain terminated in this state
        self.parent_action = parent_action
        self.n = 0
        self.model = model
        
        self.evaluate()
        # Child actions
        self.na = na
        self.child_actions = [Action(a,parent_state=self,Q_init=self.V) for a in range(na)]
        self.priors = model.predict_pi(index[None,]).flatten()
    
    def select(self,c=1.5):
        ''' Select one of the child actions based on UCT rule '''
        UCT = np.array([child_action.Q + prior * c * (np.sqrt(self.n + 1)/(child_action.n + 1)) for child_action,prior in zip(self.child_actions,self.priors)]) 
        winner = argmax(UCT)
        return self.child_actions[winner]

    def evaluate(self):
        ''' Bootstrap the state value '''
        self.V = np.squeeze(self.model.predict_V(self.index[None,])) if not self.terminal else np.array(0.0)          

    def update(self):
        ''' update count on backward pass '''
        self.n += 1

class Action():
    ''' Action object '''
    def __init__(self,index,parent_state,Q_init=0.0):
        self.index = index
        self.parent_state = parent_state
        self.W = 0.0
        self.n = 0
        self.Q = Q_init
                
    def add_child_state(self,s1,r,terminal,model):
        self.child_state = State(s1,r,terminal,self,self.parent_state.na,model)
        return self.child_state
        
    def update(self,R):
        self.n += 1
        self.W += R
        self.Q = self.W/self.n

Next, we specify an MCTS object (below). Due to the tree search, Alpha Zero is a clear model-based approach. To perform the tree search we need a model from which we can sample, and which we can return to a previous state if needed. We will work from the OpenAI Gym environment, which does not provide this functionality by default. Instead, our workhorse will be the copy.deepcopy() function, which allows us to fully duplicate an environment. If we repeatedly do this at the root of the tree, then we can repeatedly roll-out the domain from the root, as required for MCTS. For Atari 2600 games, it turns out that copying is rather computationally expensive. Therefore, we make a workaround based on specific Atari Learning Environment (ALE) helper functions to that quickly save and restore game states.

The core method is the the MCTS.search() function, which repeatedly performs the select, expand, evaluate and back-up routines. Where standard MCTS would use a (random) roll-out for the evaluate step, in AlphaZero we instead plug in a prediction from our value network (see the State.evaluate() method, which gets called in the expand step Action.add_child_state()).

In Alpha Zero, there are two other important methods necessary in the MCTS object:

1. ** Computing training targets **: After the tree search finished, we want to compute new training targets for both our policy and value network. This is done in the return_results() method.
2. ** If possible, re-use a part of the previous tree **: When we start the next tree search, we may re-use the subtree below the action that we actually picked. This is ensured in the MCTS.forward() method. If possible, then we set the new root to the state below the action that we have actually chosen in the domain (self.root = self.root.child_actions[a].child_state).

class MCTS():
    ''' MCTS object '''

    def __init__(self,root,root_index,model,na,gamma):
        self.root = None
        self.root_index = root_index
        self.model = model
        self.na = na
        self.gamma = gamma
    
    def search(self,n_mcts,c,Env,mcts_env):
        ''' Perform the MCTS search from the root '''
        if self.root is None:
            self.root = State(self.root_index,r=0.0,terminal=False,parent_action=None,na=self.na,model=self.model) # initialize new root
        else:
            self.root.parent_action = None # continue from current root
        if self.root.terminal:
            raise(ValueError("Can't do tree search from a terminal state"))

        is_atari = is_atari_game(Env)
        if is_atari:
            snapshot = copy_atari_state(Env) # for Atari: snapshot the root at the beginning     
        
        for i in range(n_mcts):     
            state = self.root # reset to root for new trace
            if not is_atari:
                mcts_env = copy.deepcopy(Env) # copy original Env to rollout from
            else:
                restore_atari_state(mcts_env,snapshot)            
            
            while not state.terminal: 
                action = state.select(c=c)
                s1,r,t,_ = mcts_env.step(action.index)
                if hasattr(action,'child_state'):
                    state = action.child_state # select
                    continue
                else:
                    state = action.add_child_state(s1,r,t,self.model) # expand & evaluate
                    break

            # Back-up 
            R = state.V         
            while state.parent_action is not None: # loop back-up until root is reached
                R = state.r + self.gamma * R 
                action = state.parent_action
                action.update(R)
                state = action.parent_state
                state.update()                
    
    def return_results(self,temp):
        ''' Process the output at the root node '''
        counts = np.array([child_action.n for child_action in self.root.child_actions])
        Q = np.array([child_action.Q for child_action in self.root.child_actions])
        pi_target = stable_normalizer(counts,temp)
        V_target = np.sum((counts/np.sum(counts))*Q)[None]
        return self.root.index,pi_target,V_target
    
    def forward(self,a,s1):
        ''' Move the root forward '''
        if not hasattr(self.root.child_actions[a],'child_state'):
            self.root = None
            self.root_index = s1
        elif np.linalg.norm(self.root.child_actions[a].child_state.index - s1) > 0.01:
            print('Warning: this domain seems stochastic. Not re-using the subtree for next search. '+
                  'To deal with stochastic environments, implement progressive widening.')
            self.root = None
            self.root_index = s1            
        else:
            self.root = self.root.child_actions[a].child_state

Agent

Finally, we put everything together in an agent() function. The agent initializes networks and environment, iteratively performs MCTS and neural network training, and stores the episode returns.

def agent(game,n_ep,n_mcts,max_ep_len,lr,c,gamma,data_size,batch_size,temp,n_hidden_layers,n_hidden_units):
    ''' Outer training loop '''
    episode_returns = [] # storage
    timepoints = []
    # Environments
    Env = make_game(game)
    is_atari = is_atari_game(Env)
    mcts_env = make_game(game) if is_atari else None

    D = Database(max_size=data_size,batch_size=batch_size)        
    model = Model(Env=Env,lr=lr,n_hidden_layers=n_hidden_layers,n_hidden_units=n_hidden_units)  
    t_total = 0 # total steps   
    R_best = -np.Inf
 
    with tf.Session() as sess:
        model.sess = sess
        sess.run(tf.global_variables_initializer())
        for ep in range(n_ep):    
            start = time.time()
            s = Env.reset() 
            R = 0.0 # Total return counter
            a_store = []
            seed = np.random.randint(1e7) # draw some Env seed
            Env.seed(seed)      
            if is_atari: 
                mcts_env.reset()
                mcts_env.seed(seed)                                

            mcts = MCTS(root_index=s,root=None,model=model,na=model.action_dim,gamma=gamma) # the object responsible for MCTS searches                             
            for t in range(max_ep_len):
                # MCTS step
                mcts.search(n_mcts=n_mcts,c=c,Env=Env,mcts_env=mcts_env) # perform a forward search
                state,pi,V = mcts.return_results(temp) # extract the root output
                D.store((state,V,pi))

                # Make the true step
                a = np.random.choice(len(pi),p=pi)
                a_store.append(a)
                s1,r,terminal,_ = Env.step(a)
                R += r
                t_total += n_mcts # total number of environment steps (counts the mcts steps)                

                if terminal:
                    break
                else:
                    mcts.forward(a,s1)
            
            # Finished episode
            episode_returns.append(R) # store the total episode return
            timepoints.append(t_total) # store the timestep count of the episode return
            if R > R_best:
                a_best = a_store
                seed_best = seed
                R_best = R
            print('Finished episode {}, total return: {}, total time: {} sec'.format(ep,np.round(R,2),np.round((time.time()-start),1)))
            # Train
            D.reshuffle()
            for epoch in range(1):
                for sb,Vb,pib in D:
                    model.train(sb,Vb,pib)
    # Return results
    return episode_returns, timepoints, a_best, seed_best, R_best

Experiments

OpenAI Gym compatibility

Our implementation is compatible with environments of the OpenAI Gym that

• have a discrete action space. (See here for our extension of Alpha Zero to continuous action space.)
• allow for copy.deepcopy() on the Environment class. This excludes the Box2D subclass of Gym.
• are deterministic. The MCTS implementation does not support a stochastic transition function (it only considers a single child state of every action), for which we would need something like ‘progressive widening’.

We mostly experimented with the discrete ‘Classic control’ domains, such as CartPole-v0, Acrobot-v1 and MountainCar-v0, and with deterministic Atari games (RAM version), e.g. Breakout-ramDeterministic-v0.

Rescaling of reward functions

Alpha Zero was implemented in two-player games, which you may either win or loose (or draw). This bounds the total return, usually beween [0,1], or [-1,1]. Thereby, it is relatively intuitive to specify the exploration constant in the UCT exploration formula. However, many single-player games have total returns on much larger scales (for example, the classic control environments have returns in [0,200] or [-500,0]. This does not fundamentally alter the task, but

• It is much harder to guess an appropriate UCT formula constant.
• Neural networks learn easiest on a normalized output.

For the classic control environments, we provide a small environment wrapper that normalizes or reparametrizes the reward function. These may be called by adding either a ‘s’ or ‘r’ to the domain specification, e.g. CartPole-v1r. For the Atari environments, each reward is clipped to [-1,1] by default (note that this does not clip the return, i.e. total reward per episode, but generally does bring it to a smaller range).

Results on CartPole

Below is a picture of a learning curve on CartPole. This can be replicated by calling python3 alphazero.py --game CartPole-v0r --window 10 --n_ep 100 --temp 20

Discussion

Data efficiency

This blog post provides a baseline implementation of Alpha Zero. However, it is not trivial to apply this to a large Atari game. The first deep RL paper in Atari 2600 (the eventual Nature version) trained each game on roughly 10 to the power 8 frames. In comparison, Alpha Zero trains 4.9 million games of ~300 moves with 1600 MCTS steps per move, making a total of roughly 10 to the power 12 environment simulations. That makes a single Alpha Zero run on Go equal about 10000 full Atari runs. And while the tree search can itself be quite fast, a single step in an Atari environment is rather slow itself (the simulator is slow). In summary, while the tree search does stabilize learning, it is actually quite data hungry, and evaluating performce will require quite some computational effort (Note that the code is neither optimized nor paralellized either).

Why does iterated search work?

To conclude this blog post, I will quickly identify a few potential reasons of why this works well. I will first identify some problems of classic RL and classic tree search.

• Classic RL is usually very unstabe (may not converge).

• Classic RL has poor exploration

• Classic search does not generalize (keeps all information in local nodes), and thereby intractable in large problems. Transposition tables only partially solve this (as they do not generalize) and do not scale either.

My hypothesis is that iterated search and deep learning (partially) solves these problems. Compared to standard 1-step RL, the MCTS procedure keeps information locally somewhat longer. The benefit is that we may compute more stable targets for our network to train on. Moreover, we can compute our new value and policy estimates based on a set of one- and multi-step targets, which helps to smooth out local generalization errors in the current value function. From the tree seach perspective, the neural networks add generalization capacity, which does implicit/automatic subtree merging and generalization.

There is much more open work in this direction, which I may cover in a future blog post.